Polymer Characterization Symposium
Presented before the Mark Twain Section
American Chemical Society
34th Midwest Regional Meeting
Quincy, October 27-29, 1999
125. AN IMOMO APPROACH TO CALCULATE THE THERMAL STABILITY OF POLYMERS: APPLICATION OF QUANTUM MECHANICS TO A "WEAR" PROBLEM
Ernest Chamot*
Chamot Laboratories, Inc.
530 E. Hillside Rd.
Naperville, IL 60540 USA
Boleslaw Porankiewicz
Department of Woodworking Machinery and Industrial Installations
Agricultural University of Poznan
Wojska Polskiego 38/42
60 627 Poznan, POLAND
High Temperature Corrosion (HTC) is a wear problem for the furniture industry, that is known to correlate with the thermal stability of the polymeric coating applied to particle board. A method to accurately calculate the energy barriers for bond dissociation in polymers has been developed, based on AM1 Semiempirical and BLYP/DZVP Density Functional calculations. This method was used to analyze the possible initiation reactions for thermal degradation of the major components of coated particle board: cellulose, lignin, Melamine-Formaldehyde Resin, and Urea-Formaldehyde Resin. The chemical features that control the thermal stability of each polymer have been identified, and 1st order thermal decomposition temperatures calculated. The calculated decomposition temperatures are consistent with experimental results over 14 orders of magnitude variation in time scale. The method for calculating the thermal stability of polymers, and its application to provide a promising lead for solving the HTC problem will be discussed.
Research that combines different disciplines or specialties frequently offers the opportunity to make dramatic progress in solving a practical problem. Research into a "High Temperature Corrosion" problem started as a problem in tribology, but turned out to be a chemical problem as well, involving polymer chemistry and computational chemistry in the research project.
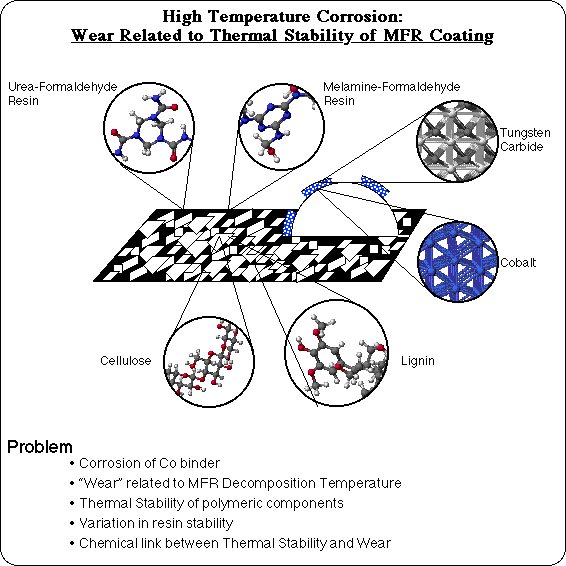
High Temperature Corrosion (HTC) is a wear problem in the secondary wood products industry. Particle board is used to fabricate a variety of products, by cutting large sheets into the appropriately shaped pieces. Particle board is composed of chips of wood, glued together with a Urea-Formaldehyde Resin (UFR). Wood, of course, is primarily composed of cellulose (a regular polymer of glucose) and lignin (an ill-defined polymer of coniferyl alcohol type repeat units). Another polymer, Melamine-Formaldehyde Resin (MFR), is used as a coating to provide a smooth, decorative finish to make furniture quality particle board, such as is commonly used in computer tables. There is an anomalous wear problem with milling MFR coated particle board, however. Normally a milling operation processes a great deal of MFR coated particle board without interruption. But sporadically there are unexplained episodes of excessive wear of the milling tool's cutting edge, and the assembly line must be shut down repeatedly to replace the cutting tool. The lost production can make this a costly problem.

The cutting edge of the milling tool is typically a composite material composed of tungsten carbide grains, which are hard and not easily abraded, held together in a cobalt binder. Examination of the worn cutting edge during one of these episodes, shows that the cobalt has been etched and corroded out from around the tungsten carbide grains. This loss of material is a chemical process, and has a synergistic effect with the mechanical processes of friction and abrasion to lead to a severe wear situation: the hard tungsten carbide grains are no longer held securely, and are more easily removed by mechanical contact. What's intriguing, is that this corrosive wear turns out to correlate very well with the thermal decomposition temperature of the Melamine-Formaldehyde Resin, as measured by Thermal Gravimetric Analysis (TGA): samples with reduced thermal stability tend to have this corrosive wear problem, and samples with higher decomposition temperatures tend not to. Hence, the term "High Temperature Corrosion." In order to understand why wear would be related to the decomposition temperature of the MFR coating, answers are needed to the questions, "What is the thermal stability of each of the polymeric components?" "Why is there variability in the stability of a resin?" and ultimately, "What is the link between thermal stability and wear?"
Thermal degradation itself is an extremely complex process. Pyrolysis of simple saturated hydrocarbons, for instance, starts with a bond breaking reaction to form free radicals as primary products. Then these free radicals undergo a multitude of secondary reactions: rearrangement reactions, b-scission, H-elimination, H-abstraction, olefin addition, etc., and ultimately abstract hydrogen from unreacted hydrocarbon molecules to initiate them into the pyrolysis reaction cycle. Modeling the entire process would be a daunting task, but it would be necessary to consider all of the reaction barriers in order to predict product distributions, for instance. But thermal stability, in terms of the onset temperature observed in a TGA experiment, does not necessarily involve the entire degradation process, it is a matter of whether or not thermal degradation will start at a given temperature. To predict the onset of thermal degradation, it is important to realize that none of the free radical reactions can take place until after the first step: the bond homolysis step. This initiation reaction is the key to limiting thermal stability, and that makes this whole problem tractable.
In a polymer there are many different bonds, and there may also be many different types of bonds, that can break. If this ensemble of different bonds were represented in a bulk material of small molecules, there would be a distribution of bonds broken: thermal energy would be distributed, with some molecules having enough energy to break some of the stronger bonds, and some only having enough energy to break the weakest bond. But with all of the bonds in a single polymer chain, there will not be involvement of more than one bond in the initiation step: once one bond in the polymer molecule has dissociated, degradation of that polymer chain has begun. Thermal energy will distribute itself relatively rapidly along the polymer chain, so that all of the backbone bonds are exposed to the energy at some point (as a stretching vibration, for instance). The bond which will break first, of course, is the one that is the weakest link in the chain. So the question of what limits the thermal stability of polymers becomes, "What is the weakest bond in the polymer chain?" and specifically "What is its bond dissociation energy?" That is what that will limit the stability of a polymer chain.

Another way that polymers differ from small molecules, is in their bond dissociation profile. In a small molecule in vacuum, as a bond dissociates the energy will rise to level off and approach a limit that is equal to the sum of the energies of the separated free radicals. This is traditionally considered to be a process that does not have a transition state. In the case of a polymer, though, this is an oversimplification, and it is not sufficient to look up the strength of a C-C single bond, for instance, in a table or text book. In the reaction profile for dissociation of an anti C-C bond in a segment of isotactic PolyPropylene (PP), for example, the energy actually rises to a maximum and then drops a bit (although only by a few kcals) as the segment finishes separating into free radicals: there is a low transition state for this reaction.1 The difference, is that in a polymer there are interactions along the length of the chain. There are no strong interactions, like H-bonding, in the case of PP, but isotactic polypropylene adopts a helical conformation, and the steric interactions between one turn of the helix and the next are strong enough to affect bond strengths. In order for the 2 carbons to flatten out and change geometry from the tetrahedral sp3 to the trigonal planar sp2 free radical geometry, the ends of the polymer have to disengage. This delays rehybridization until a longer distance separates the two carbons, which in turn has an effect on the energy. All of the backbone bonds in PP would be identical (trisubstituted, aliphatic, C-C single bonds), except that they are rotated alternately in trans and gauche conformations in the helix. The steric interaction along the chain is enough to make a difference in stability between the anti and gauche bonds, with the barrier to breaking a gauche bond 2.5 kcal/mol lower than for breaking an anti bond. That corresponds to a factor of 10 difference in half-life, at the melting point of polypropylene!

This effect is not adequately represented with small model compounds. A PP tetramer, for instance, does not have a full turn of the helix on either side of the bond being broken. So calculated Bond Dissociation Energies (BDE's) do not show a difference between the gauche and anti backbone bonds. Ab initio Hartree-Fock or Density Functional calculations are more accurate than Semiempirical calculations, but on a tetramer they too only reflect small molecule behavior: the gauche bond is no easier to break than the anti bond. So any simulation of bond dissociation in polymers will have to use a large enough model compound to realistically represent the polymer environment about that bond.
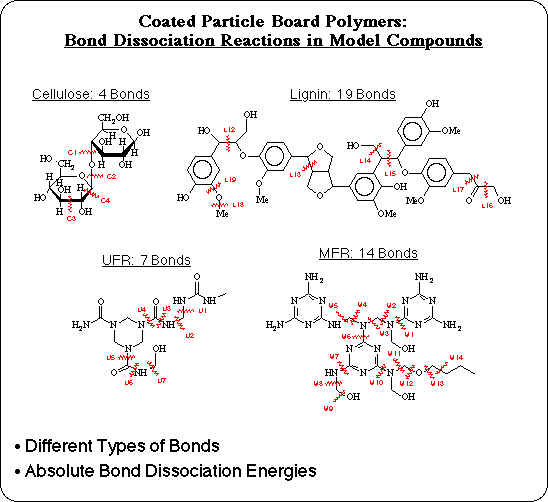
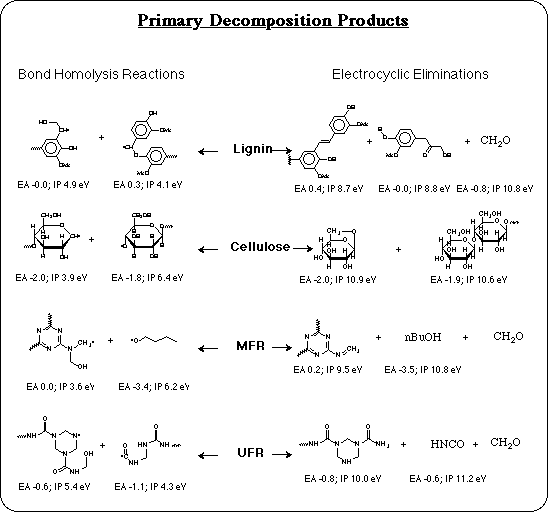
A set of model compounds has been developed to realistically represent each of the major components and each of the bond types in MFR coated particle board: an alpha-D-glucose dimer to represent cellulose, a coniferyl alcohol pentamer to represent lignin, a urea-formaldehyde tetramer to represent UFR, and a melamine-formaldehyde trimer to represent MFR. Unlike polypropylene, relative bond dissociation energies are insufficient to determine which is the weakest bond in these systems. In order to compare the 18 different types of bonds and 4 different polymers in the composite, accurate absolute bond dissociation energies are necessary.
When asked, "When studies show that half of back problems respond best to medication, why do surgeons almost always recommend surgery?" an orthopedic surgeon once replied, "Well, when you're carrying around a hammer, everything starts to look like a nail." This may be an appropriate strategy for developing a specific Computational Chemistry method, but our interest is in solving practical problems. To effectively apply Computational Chemistry to practical problems, it is necessary to match the right computational tool (the "hammer") to the problem: in this case, calculating a series of bond dissociation energies in fairly large model compounds.

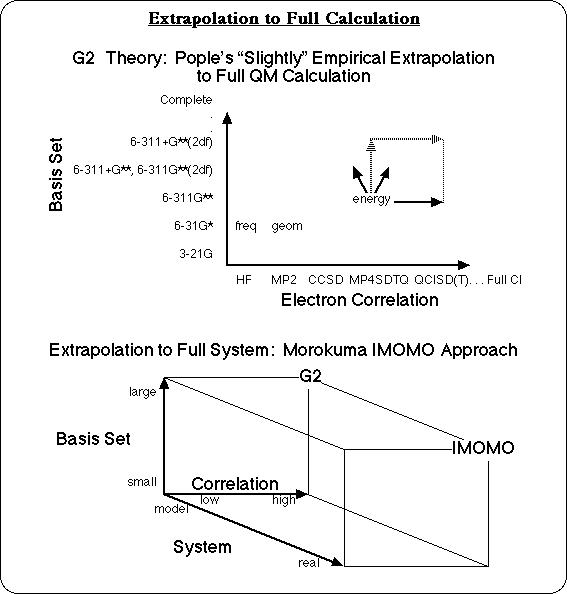
The most accurate energies would probably come from G3 calculations. Individual bond dissociation energies from G3 calculations are typically accurate to about 2 kcal/mol for bonds between two heavy atoms. The problem is that there are a lot of these reactions to analyze, and G3 calculations on even medium sized molecules would take some very "heavy iron," (ie. a large computer) and a lot of patience. Ann Chaka at Lubrizol is fond of saying that, "there are only 3 time scales for solving industrial problems: over coffee, over lunch, or over night." But a G3 calculation for a small molecule is a computational experiment that might run "over vacation," and a G3 calculation on an industrial polymer, would still be running at the end of the Stellar Era,2 and continue well into the heat death of the universe! So this problem is not suitable for G3 calculations.
Gradient Corrected Density Functional calculations are almost as accurate for individual bond dissociation energies as G3 calculations: within about 3 kcal/mol with the Becke and Lee-Yang-Parr functionals,3, 4 for instance. They have the advantage of being significantly faster. Semiempirical calculations, such as AM1, are even faster, and can be run on fairly large molecules in the "over lunch" or "over night" timeframe, but they are known to significantly under predict bond dissociation energies,5 as do ab initio Hartree-Fock3,5 calculations that do not also include correlated methods. AM1 calculations can give reasonable relative bond dissociation energies for similar types of bonds, however, and with a little finesse, the results of calculations run on the Semiempirical time scale can be used to approximate Density Functional calculation accuracy.
An effective strategy to approximate the result of a calculation that would be more accurate but is not feasible, is to extrapolate the high level result from two or more lower level calculations. Pople's G26 and G3 Theories themselves are based on what he calls a "slightly empirical" extrapolation to a full calculation. The results of calculations with smaller basis sets, and lower levels of correlation are combined with correction factors to extrapolate to the complete basis set and full CI calculation, for small molecules. Morokuma takes this approach one step further, in order to get high level calculation results on large molecular systems. In the Integrated Molecular Orbital Molecular Orbital (IMOMO) method,7 a high level MO theory calculation and a lower level MO theory calculation on a small model compound are combined with the results of a low level MO theory calculation on the large molecule. These two vectors are used to extrapolate to the result of the high level MO theory calculation on the large molecule. Other researchers have their own versions of this strategy: Truhlar's Correlated Capped Small System5 method, Melius' Bond Additive Correction8 method, Irikura's method for correcting bond energies,9 etc. The IMOMO strategy has been applied in this work to calculating accurate Bond Dissociation Energies (BDE's) for polymers.
Density Functional Calculations with the Becke and Lee-Yang-Parr gradient corrections were used as the high level MO theory, and Semiempirical calculations with the AM1 Hamiltonian were used as the lower level MO theory. The true heat of reaction (in this case, the BDE) is assumed to be separable into the calculated heat of reaction, plus an error due to the limitation of the computational method, plus an error due to the use of a model compound. First, the size of a model compound necessary to minimize the error due to the model was determined. Dissociation of the C-C bond adjacent to the ether oxygen in MFR, for instance, was simulated at the AM1 level, with the program MOPAC, for a series of smaller and smaller model compounds. With the largest model compound, including 2 melamine-formaldehyde units, a BDE of 62.5 kcal/mol is calculated. The simpler model, containing only one melamine-formaldehyde unit, is calculated to have the same BDE. But a model compound with only an aminoethanol group to represent the melamine-formaldehyde unit has a slightly lower BDE, and using ethanol as the model compound clearly no longer represents dissociation of the C-C bond next to an oxygen in the polymer: the BDE is 5 kcal/mol too high. It was generally found to be necessary to include the atoms at least 3 bonds away from the bond being broken, and preferably including at least one whole melamine-formaldehyde unit in the model compound, in order to realistically represent the polymer.

The next step was to quantify the error inherently due to the MO method with the appropriate model compound. The C-C BDE for the model compound with a full melamine-formaldehyde residue was calculated with Density Functional Theory, with the BLYP functional and the DZVP basis set, using the DGauss program. As expected, the more accurate BLYP calculation confirmed that the Semiempirical calculation substantially under predicts the BDE, and quantified the difference as 19.6 kcal/mol for this bond. This difference was taken as the error due to the AM1 method for this type of C-C bond, and used to correct the corresponding BDE's calculated by AM1 in the large model compound, to approximate BLYP quality BDE's. A similar pair of Semiempirical and Density Functional BDE calculations was carried out for each type of bond homolysis with medium sized model compounds (10-29 heavy atoms), to derive AM1 to BLYP correction factors for 18 different types of bond. These corrections were then applied to the results of Semiempirical AM1 calculations on the large model compounds, to extrapolate BLYP quality Bond Dissociation Energies.
The calculated results are shown for 32 of the bond dissociation reactions analyzed for cellulose, lignin, UFR, and MFR: the AM1 Semiempirical BDE's, the corresponding correction factors for each, and the extrapolated BLYP quality BDE's. Several corrections are on the order of 15-20 kcal/mol, as expected, but some bond dissociations don't require much correction, such as the dissociation of C-O bonds. This demonstrates that the error in AM1 BDE's is only systematic within the same bond type.

The set of consistent, accurate BDE's lead to our first new insight into the mechanism of High Temperature Corrosion. Previously, it had been assumed that the mechanism linking the stability of the MFR sample to corrosive wear, must be that decomposition of the MFR generated free radicals, and free radicals would react with oxygen to start oxidation reactions, or start electron transfer reactions, etc. The friction between the cutting tool and the wood piece generates heat, and if the decomposition temperature of a less stable batch of MFR is below the temperature experienced by the cutting edge, the resin will start generating free radicals. More stable MFR coatings would not decompose at the cutting edge temperature, so there would be no source of free radicals. But High Temperature Corrosion can't just be due to the presence of free radicals, because lignin, a component of the wood, will be generating free radicals long before even the most stable MFR coatings. So HTC must be the result of a specific reaction.
A frequency calculation is normally done as part of each geometry optimization to verify that the molecule is in a stable geometry. These frequencies were used to calculate the entropy, and the enthalpies and entropies were used to calculate the free energy, delta-Gdiss, for each bond dissociation reaction. This thermodynamic barrier was used to apply simple Transition State Theory, by using it as an approximation of the activation energy in the Arrhenius equation. Preexponential factors, A, for unimolecular C-C and C-N bond dissociations are typically on the order of 1016 sec-1, so this value was used for A, and 1st order rate constants were calculated for each reaction (at 500° C for example) via: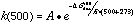
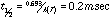
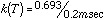
The individual decomposition temperatures provided an insight into the conditions responsible for HTC. There has been a lot of controversy as to what temperature is actually attained at the surface of the cutting tool where High Temperature Corrosion takes place: the contact time is very short, the cutting edge moves at a high linear velocity through the particle board, and the force is concentrated at a sharp point, so friction is high, and the heat is localized. Estimates have ranged from a couple hundred degrees to 1000° C. The range of calculated decomposition temperatures suggests that, for the thermal stability of MFR to be involved, the estimates of a couple hundred degrees are more reasonable: 300-400° C.10
Decomposition temperatures were also calculated on the time scale of a Thermal Gravimetric Analysis (TGA): about 50°/min. temperature rise. On this longer time scale, decomposition temperatures are significantly lower, and can be compared directly with experiment. Whenever molecular modeling is used to apply theory, the method must be validated before the predictions can be relied upon, to make sure one is simulating the system realistically. In this instance it was necessary to validate the use of simple Transition State Theory, and to determine how accurately BDE's translate into decomposition temperatures. The calculated decomposition temperatures for MFR and UFR are very consistent with the reactions observed in TGA experiments. They fit perfectly under the observed decomposition peak.
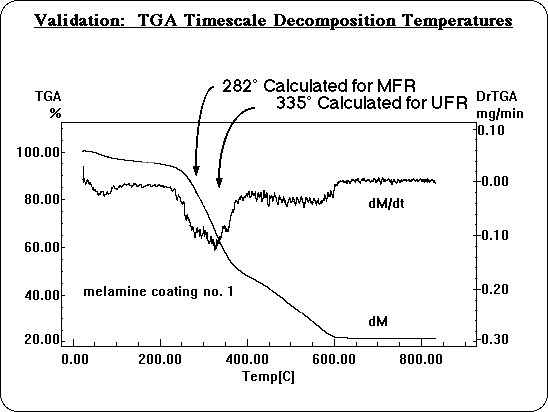
Likewise, the calculated decomposition temperatures for lignin and cellulose are consistent with the experimental TGA of a wood sample, although the wood TGA is more complex. Wood adsorbs water which is desorbed at low temperatures and partially obscures the region where the decomposition of lignin is predicted. There is also a well known decomposition reaction of cellulose that does not involve free radicals, the electrocyclic elimination of levoglucosan, responsible for another peak around 340° C. The third decomposition peak in the TGA of wood, however, includes the range where cellulose is predicted to decompose by bond homolysis, agreeing with these calculations.

Finally, one more time scale was available for comparison. Recently, FTIR analysis of a sample of wood from a 7th century Japanese temple11 has been reported to show that the lignin decomposed during the intervening centuries. There may be oxidation and other factors involved, of course, but the decomposition temperature of lignin on the temple time scale was calculated too, for comparison. It was found to be below ambient temperature, so calculated decomposition temperatures are consistent with this observation as well. Even using simple Transition State Theory with estimated preexponential factors, calculated decomposition temperatures based on the AM1/BLYP corrected BDE's are consistent with experimental data over 14 orders of magnitude variation in time scale!
The composite decomposition temperatures validated the IMOMO approach to modeling the thermal stability of polymers in this system. The results for individual bond dissociation reactions were next analyzed to understand the chemistry involved. In particular, "What are the primary decomposition reactions and their products, that might be responsible for the corrosion process?"
The lowest energy bond dissociation reaction in the MFR model compound, is calculated to be homolysis of the C-O bond of a butyl ether. This group is not part of melamine, nor does it come from formaldehyde. It comes from condensation with butyl alcohol that is used by some manufacturers as a processing aid to keep the system fluid as the monomers condense. As the condensation of monomers proceeds, most of the butyl alcohol is displaced and driven off along with the water vapor. But some residual butyl alcohol is known to remain incorporated as butyl ether. These calculations predict that when any butyl ether residues remain, their C-O bond will be the weak link that limits the thermal stability of the resin. This explains the variability in the thermal stability of MFR coatings: resins from a manufacturer that uses butyl alcohol, but doesn't completely eliminate it in their process, will be less stable and could have an HTC problem. So an obvious solution is to avoid the use of butyl alcohol in the MFR process.
Another solution would be to control the process, so as to minimize residual butyl ether. Some manufacturers make a special grade of MFR with a process called "hardening." Typically an acid catalyst is added and heating is prolonged to force additional crosslinking. This would displace the residual butyl alcohol, as well as eliminating additional water, as condensation is driven to completion. It might seem that deliberately making a material harder and adding acid would increase wear, but in this case our analysis of the chemistry of HTC predicts that "hardening" should result in a more thermally stable resin, which should in turn reduce the wear due to HTC. Additional wear experiments were carried out with "Hardened" MFR samples, and these confirmed our prediction: hardened resins did not have the unusual wear associated with High Temperature Corrosion! A priori, "hardening" the MFR to reduce wear would be a counter intuitive solution, but it follows directly from our analysis.
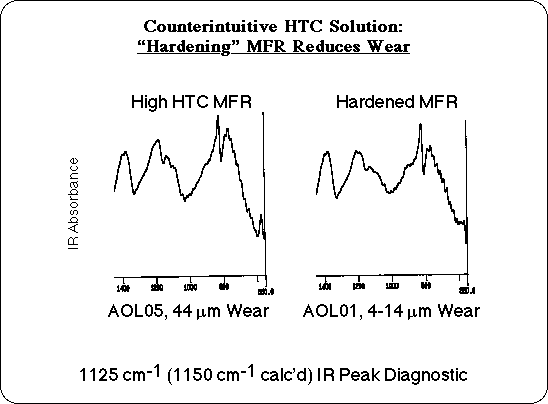
Once the critical structural feature had been tentatively identified, its presence in high wear samples could be verified analytically. The Infrared (IR) spectra of the particle board components were calculated from the vibrational frequencies and transition dipoles of the model compounds. The theoretical absorption maxima of the butyl ether group were identified, and compared with experimental IR spectra. The calculations predict one of the characteristic vibrations to absorb between 1125 and 1150 cm-1, and there is in fact a small peak observed in this region of the experimental IR of samples that exhibited excess wear. This peak tends to be smaller or missing in the IR spectra of hardened MFR and in MFR samples that have low wear. This region of the experimental IR is probably too complex to quantify the residual butyl alcohol content based on the intensity of this absorption, but the presence of this peak in the IR could serve as a diagnostic tool to flag MFR coated particle board that may have an HTC wear problem.
In conclusion, polymer thermal stability can be predicted based on calculated bond dissociation energies, relying on the fact that bond dissociation will determine the onset of thermal degradation, and that in polymers it is the weakest link in the chain that will limit the thermal stability of the entire molecule. An Integrated Molecular Orbital Molecular Orbital approach has been developed, using Density Functional Calculations with the BLYP Generalized Gradient Approximation as the high level MO Theory for accuracy, and using AM1 Semiempirical calculations as the lower level MO Theory, in order to model realistic model compounds that accurately represent the polymer. A set of correction factors was developed, between AM1 and BLYP calculations. With Bond Dissociation Energies calculated in this way, polymer thermal decomposition temperatures can be calculated that are consistent with experiment over 14 orders of magnitude variation in time scale, the initial stages of the High Temperature Corrosion mechanism have been identified, and a counter intuitive solution to HTC has been found.
Not only has this research been multidisciplinary, but the funding has been a cooperative effort as well. Funding has been provided by a joint American-Polish research fund provided by the United States Department of Agriculture, and the Maria Sklodowska-Curie Joint American-Polish Research Fund.
The assistance of Oxford Molecular Group, Inc. in providing access to DGauss on a Cray supercomputer to run the Density Functional calculations is gratefully acknowledged.
The authors also gratefully acknowledge use of the Center for Computational Science and Technology at Argonne National Laboratories for use of their workstations. The CCST is funded principally by the US Department of Energy, Mathematical, Information and Computational Sciences Division (ER-31).
1 E. Chamot, A. Rollin, M. Schoenberg, and B. Firth, "Probing Polyolefin Stabilities by Semiempirical Methods," presented at the Central Regional American Chemical Society Akron Meeting, May 31-June 2, 1995.
2 6x1014 years for extrapolation to 100,000 mw PE from naphthalene calculation. Assumes N7 scaling of limiting MP4 calculation in G3, 106 speed increase w/ molecular electronics for computers, and Stellar Era 1014 years.
3 B. Jursic, THEOCHEM, 366(1-2), 103-8, (1996); B. Jursic & R. Martin, Int. J. Quantum. Chem., 59(6), 495-501 (1996).
4 J. Cioslowski, G. Liu, & D. Moncrieff, J. Amer. Chem. Soc., 119(47), 11452-7 (1997).
5 M. Noland, E. Coitino, & D. Truhlar, J. Phys. Chem. A, 101(7), 1193-7 (1997).
6 L. Curtiss, K. Raghavachari, G. Trucks, & J. Pople, J. Chem. Phys., 94, 7221 (1991).
7 S. Humbel, S. Siever, K. Morokuma, J. Chem. Phys., 105, 1959 (1996).
8 P. Ho, M. Coltrin, J. Binkley, & C. Melius, J. Phys. Chem., 89, 4647-54 (1985); R. Berry, D. Burgess, M. Nyden, M. Zachariah, C. Melius, & M. Schwartz, J. Phys. Chem., 100, 7405-10 (1996).
9 K. Irikura, J. Phys. Chem. A, 102, 9031-9 (1998).
10 This estimate is being refined with finite element analysis, and is in good agreement with preliminary estimates of temperatures up to 450° C.
11 T. Takei, M. Hamiajimia, & N. Kamiba, "Fourier Transform Infrared Spectroscopic Analysis of the Degradation of Structural Lumber in Horyuki Temple," (1997).
