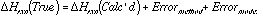
Division of Polymer Chemistry
Symposium on Stability of Plastics and Rubbers
American Chemical Society
San Diego Meeting
March, 2001

**Draft**

For Publication in Polymer Preprints
Volume 42, No. 1
March, 2001

A COMBINED MOMO ANALYSIS OF THE ONSET OF THERMAL DEGRADATION IN POLYMERS


Ernest Chamot

Chamot Laboratories, Inc.
530 E. Hillside Rd.
Naperville, Illinois 60540



Abstract

In a strictly thermal process, the thermal degradation of polymers by a free radical mechanism is initiated by a homolytic bond dissociation. This provides the initial source of free radicals which can undergo subsequent beta-scission, rearrangement, elimination, H-abstraction reactions, etc. that break the polymer down. By analyzing the Bond Dissociation Energy (BDE) of each bond in the polymer, the inherent limitations to thermal stability can be identified. A combined Molecular Orbital-Molecular Orbital (MOMO) method has been developed to accurately calculate individual, absolute BDE's for polymers, based on BLYP Density Functional and AM1 semiempirical calculations. This method provides energies accurate enough to analyze the effect of polymerization irregularities, and to predict thermal decomposition temperatures. The development and application of this method to the commercialization of a polyolefin process and the solution of a "wear" problem in the furniture industry will be discussed.

Introduction

Thermal degradation is an extremely complex process. In the absence of specific reactions, such as elimination,1 retro Diels-Alder, Ene reaction, etc.,2 thermal decomposition proceeds via a radical mechanism, initiated by homolysis of a bond. This generates a pair of free radicals as primary products, which can then undergo a multitude of secondary reactions: rearrangement, beta-scission, elimination, H-abstraction, olefin addition, etc., and ultimately abstract hydrogen from unreacted molecules to initiate them into the pyrolysis reaction cycle. Modeling all of the reactions would be necessary in order to simulate product distributions, but predicting thermal stability, in terms of the onset temperature observed in a Thermal Gravimetric Analysis for instance, does not require simulating the entire degradation process. It is a matter of whether or not thermal degradation will start at a given temperature. Since none of the free radical reactions can take place until after the bond homolysis step, this initiation reaction is the key to limiting thermal stability.

In a polymer there are many different bonds and types of bonds, that can break. If this ensemble of different bonds were represented in a bulk material of small molecules, there would be a distribution of bonds broken But with all of the bonds in a single polymer chain, there will not be a distribution of bonds broken in the initiation step: once one bond in the polymer molecule breaks, the molecular weight of that polymer chain has been reduced and degradation has begun The bond that will tend to break first is the one that forms the weakest link in the chain. This is why most polymers decompose at a temperature substantially lower than comparable small molecules when there are irregularities that can act as weak points where degradation starts.3 The factor that limits polymer thermal stability is the strength of the weakest bond in the polymer chain.

Polyolefins are some of the largest volume commodity organic chemicals industry produces, and are produced with a variety of processes. This results in a wide range of polyolefin grades, differing in tacticity, morphology, degree of branching, molecular weight distribution, etc. They also differ in thermal stability and can require significantly different stabilizer formulations.

Polymeric resins, Melamine-Formaldehyde Resin (MFR) and Urea-Formaldehyde Resin (UFR), are used in the secondary wood products industry to make furniture quality particle board. There is an anomalous wear problem with milling MFR coated particle board, however. Sporadically, there are unexpected episodes of excessive wear of the milling tool, causing the assembly line to be shut down to replace the cutting edge. This wear is unusual, in that it is a corrosive wear that correlates strongly with the thermal decomposition temperature of the MFR coating, as measured by Thermal Gravimetric Analysis: samples with reduced thermal stability tend to have this corrosive wear problem, and samples with higher decomposition temperatures tend not to. Hence, it has been termed "High Temperature Corrosion" (HTC).4

A combined Molecular Orbital-Molecular Orbital (MOMO) method has been developed to accurately calculate absolute Bond Dissociation Enthalpies (BDE's) for polymers, based on BLYP Density Functional and AM1 semiempirical calculations. This method has been used to analyze the effect of polymerization irregularities on the thermal stability of polyolefins, and to predict thermal decomposition temperatures of the polymeric components of particle board.

Computational Details

An ensemble of realistic model compounds, representing each bond in each polymer was constructed, and geometries determined by molecular mechanics. Isotactic PolyPropylene (i-PP) model compound geometries were optimized by first carrying out an exhaustive conformational search with the MM2 force field. The amorphous polymer (MFR, UFR, and lignin) model compound geometries were sampled with a combination of conformational searches and molecular dynamics simulations with the MM2 force field at 500° K for 1 ps. The lowest energy conformations were selected as representative, and optimized further by molecular mechanics, and then semiempirically with the AM1 Hamiltonian in MOPAC. The corresponding free radicals resulting from bond homolysis were modeled with AM1 as ROHF doublets. Optimizations were continued to a GNORM of 0.1 for accurate energies, and were followed by a FORCE calculation to provide thermodynamic data, and to verify that each geometry was a ground state.

For DFT calculations, AM1 geometries were reoptimized and energies calculated with the program DeGauss. The B88-LYP Generalized Gradient Approximation was used, with a DZVP basis set. A FINE numeric grid, and TIGHT criteria for SCF convergence were used, and geometries were converged to a GNORM of 5x10-4.

MOMO Methodology

In order to accurately and realistically simulate bond homolysis in a polymer, it is just as important to use a large enough model compound to reproduce the effect of long range interactions along the polymer chain, as it is to use an accurate method. Even the weak interactions along an isotactic polypropylene chain between one turn of the 3-1 helix and the next, are enough to change the energetics of bond homolysis.5

Semiempirical AM1 calculations can model large molecules and give reasonable relative bond dissociation energies for similar types of bonds, but they are known to significantly under predict bond dissociation energies,6 as do ab initio Hartree-Fock7 calculations that do not also include correlated methods. Gradient Corrected Density Functional calculations are almost as accurate for individual bond dissociation energies as G3 calculations: within about 3 kcal/mol with the Becke and Lee-Yang-Parr functionals,8 but are only practical for intermediate size molecules. To circumvent these limitations, a combined Molecular Orbital-Molecular Orbital (MOMO) method was developed to analyze polymer bond dissociation energies. This strategy is similar to the approach of Morokuma9 and others, in which accurate energies for a large system are calculated by combining the results of a lower level MO calculation on the full system with a high level MO calculation on a related small system.

Density Functional Calculations with the BLYP functional were used as the high level MO theory, and semiempirical calculations with the AM1 Hamiltonian were used as the low level MO theory. The true heat of reaction (in this case, the Bond Dissociation Enthalpy, BDE) is assumed to be separable into the calculated heat of reaction, plus an error due to the limitation of the computational method, plus an error due to the use of a model compound:



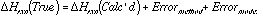
For the analysis of BDE's in polymers, the difference between the corresponding BLYP and AM1 calculations on a small model compound were used to estimate the systematic error due to the AM1 method in calculating the BDE in the polymer:



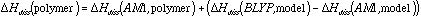
This is analogous to the general empirical corrections for ab initio BDE's developed by Irikura,10 but is more specific in that a correction is calculated for each individual bond.

A set of polymer models was developed to realistically represent each of the major components and each of the bond types in the polymers: a series of propylene and butylene octamers, an MFR trimer, a UFR tetramer, an alpha-D-glucose dimer (to represent cellulose), and a coniferyl alcohol pentamer (to represent lignin). These were modeled at the AM1 semiempirical level. Then a corresponding small model compound was modeled at both the AM1 and BLYP Density Functional level, and an AM1 to BLYP correction calculated. The small model compounds needed to include atoms at least 3 bonds away, and to consist of 10-29 heavy atoms for the corrections to converge. Correction factors for 36 different types of bond have been calculated. These corrections were then applied to the results of semiempirical AM1 calculations on the polymer model compounds, to extrapolate BLYP quality BDE's.

Results and Discussion

In the case of polyolefins, all of the backbone bonds are very similar (saturated C-C single bonds) so that the AM1 BDE errors, although large, are systematic: the same trends are observed with or without the AM1 to BLYP correction. Analysis of stereoregular isotactic PolyPropylene (i-PP) lead to the interesting prediction that, due to the alternating anti-gauche conformation of the backbone bonds in forming the known, 3-1 helical crystal structure,11 i-PP should have alternating strong and weak bonds, differing by about 2.5 kcal. This could explain the observation of "oligomers" in Mass Spectral analysis of i-PP, even when the low MW oligomers have been extracted: the i-PP may just be decomposing thermally in even monomer units.

The effect of various irregularities in i-PP (monomer inversion, monomer reversal, head-to-head or tail-to-tail coupling, 1,3-insertion, etc.) on BDE's was analyzed with the MOMO method, to determine their effect on the inherent thermal stability of polypropylene. The weakest link in a stereoregular i-PP is stronger than in propylene polymers with irregularities, but an occasional tacticity irregularity doesn't significantly weaken the chain (70.9 vs. 71.2 kcal). Orientation irregularities, however, can drop the stability by 3-5 kcal/mole. A head-to-head junction, either from a coupling reaction or from a monomer reversal, would result in a BDE of 67.8 kcal (vs. 71.2 kcal). A tail-to-tail junction would be more stable (75.6 kcal), but this would not increase the thermal stability of the polymer, since it would still be limited by the BDE of the weakest link.

A similar analysis of the bonds in polybutenes predicts that even a stereoregular, alternating i-butene/n-butene copolymer would be less stable than propylene, even with the least stable irregularity (64.2 kcal vs. 67.8 kcal). Any i-butene/i-butene combination would introduce an even weaker link in the backbone by 2-3 kcal, so it is clear that viscous polybutene is inherently less stable than i-PP.

To analyze the stability of particle board resins with respect to the High Temperature Corrosion (HTC) problem, it was desirable to relate the stability to decomposition temperatures, as well as to determine the structural features responsible for limiting thermal stability. Accordingly, the corrected BDE for each bond in each component was used to estimate the free energy of bond dissociation, Gdiss, by combining it with entropies calculated from the AM1 frequency calculations. Simple Transition State Theory turned out to be sufficient for predicting rate constants, by using this estimate as an approximation of the energy barrier in the Arrhenius equation. A typical unimolecular value of 1016 sec-1 was used for the preexponential factor, A, and 1st order rate constants were calculated for each reaction (at 500° C for example) via:



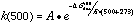
Decomposition temperatures were calculated, by deriving the equation for a half-life from the integrated rate law for a 1st order reaction, and solving for the temperature at which the half-life is equal to the time scale of the process. Decomposition temperatures calculated on the Thermal Gravimetric Analysis (TGA) timescale (50° C/min temperature rise) reproduced experimental TGA spectra of mixed Melamine-Formaldehyde Resin (MFR) and Urea-Formaldehyde Resin (UFR) very well: 282° C and 335° C calculated vs. the observed broad 250-350° C decomposition peak. Calculated decomposition temperatures on the cutting contact timescale (0.2 msec) are consistent with frictional temperatures from finite element estimates of up to 450° C. This tends to confirm the validity of these calculations.

The weakest bond in the MFR model compound that is predicted to limit its stability is the C-O bond of a butyl ether. This group is not inherently part of a Melamine-Formaldehyde Resin. It is an artifact of the use of butyl alcohol as a process aid. Residual butyl alcohol is known to sometimes remain incorporated as butyl ether. These calculations predict that whenever butyl ether residues are present, their C-O bond will be the weak link that limits the thermal stability of MFR. This explains the variability in the thermal stability of MFR coatings: relatively small amounts of butyl alcohol residues will significantly reduce the thermal stability of MFR and decomposition will result in HTC.

One impractical solution would be to avoid the use of butyl alcohol in the MFR process, but by understanding the decomposition mechanism, another solution presented itself. A special grade of MFR is made with a process called "hardening," by prolonged heating with an acid catalyst. This forces additional condensation and crosslinking, but should also displace the residual butyl alcohol. This should result in a more thermally stable resin, which would in turn reduce the decomposition processes responsible for HTC. Subsequent wear experiments with "hardened" MFR samples confirmed this prediction.

Conclusion

Polymer thermal stability can be predicted based on calculated bond dissociation energies, relying on the fact that bond dissociation will determine the onset of thermal degradation, and that the weakest link in the chain limits the thermal stability of the entire molecule. A combined Molecular Orbital-Molecular Orbital method has been developed, using BLYP Density Functional calculations as the high level MO Theory for accuracy, and using AM1 semiempirical calculations as the lower level MO Theory, in order to model polymers with realistic model compounds. A set of correction factors was developed, relating AM1 to BLYP calculations. With BDE's calculated in this way, initial fragmentation patterns, relative polymer stabilities, and polymer thermal decomposition temperatures can be calculated that are consistent with experiment.

Stereoregular isotactic polypropylene is predicted to have alternating strong and weak backbone bonds, and the irregularity that would most reduce thermal stability is formation of a head-to-head junction. Viscous polybutenes are inherently less stable than polypropylene. The initial stages of the High Temperature Corrosion mechanism have been identified, and a counter intuitive solution to HTC has been found.

Acknowledgements. Part of the funding for this research was provided by a United States Department of Agriculture, and Maria Sklodowska-Curie Joint American-Polish Research Fund. The author also gratefully acknowledges the assistance of Oxford Molecular Group, Inc., and the Center for Computational Science and Technology at Argonne National Laboratories, for providing access to DGauss on a Cray supercomputer. The CCST is funded principally by the US Department of Energy, Mathematical, Information and Computational Sciences Division (ER-31).

References.

1 Minsker, K.S.; Kolesov, S.V.; Yanborisov, V.M. Polymer Deg. and Stab. 1984, 9, 103.

2 Zubkov, V.A.; Bogdanova, S.E.; Yakimansky, A.V.; Kudryavtsev, V.V. Macromol. Theory Simul. 1995, 4, 209.

3 Munk, P. Introduction to Macromolecular Science, John Wiley & Sons, New York, 1989, p 212.

4 Stewart, H.A. Forest Products Journal 1989, 3, 25.

5 Chamot, E.; Rollin, A.; Schoenberg, M.; Firth, B. "Probing Polyolefin Stabilities by Semiempirical Methods," presented at the Central Region ACS Meeting, Akron, Ohio, May 31-June 2, 1995.

6 Noland, M.; Coitino, E.; Truhlar, D. J. Phys. Chem. A 1997, 101(7), 1193.

7 Jursic, B. THEOCHEM 1996, 366(1-2), 103; Jursic, B.; Martin, R. Int. J. Quantum. Chem. 1996, 59(6), 495.

8 Cioslowski, J.; Liu, G.; Moncrieff, D. J. Amer. Chem. Soc. 1997, 119(47), 11452.

9 Humbel, S.; Siever, S.; Morokuma, K. J. Chem. Phys. 1996, 105, 1959.

10 Irikura, K.K. J. Phys. Chem. A 1998, 102, 9031.

11 Crawford, J.W. J. Soc. Chem. Ind. 1949, 68, 201.

Return

Chamot Labs Logo
12/11/00 Ernie Chamot / Chamot Labs / Business Number / echamot@chamotlabs.com