by Ernest Chamot , Consultant with Chamot Labs, Naperville, Illinois.
This first figure includes a second visualization of the molecule that you can manipulate via a Java applet. Please wait for it to load completely. . .

|
(If your browser supports Java, you can manipulate the molecule on the right: drag slowly to rotate, shift-drag to zoom, and control-drag to move. Otherwise, click on the image on the left, to activate a helper application that can manipulate a PDB format molecule.)
Polymers find use in a wide range of applications, from milk bottles to clothing in forms ranging from engineering plastics to viscous fluids. As diverse as these applications are, all require some degree of thermal stability in addition to application specific requirements: if the polymer undergoes thermal decomposition or degradation, it may no longer have the same properties that it did initially. There may also be a concern with resistance to oxidation, irradiation, etc., but if the polymer can't survive the elevated temperatures of synthesis, processing and normal use, other modes of degradation become irrelevant.
Experimental tests are both time consuming and expensive as they require that a new polymer be actually synthesized and processed. The ability to predict thermal decomposition temperatures and to distinguish between degradation mechanisms by Computer Aided Chemistry can save significant time and money, as little or no experimental work is required.
Further, the Computer Aided Chemistry approach often provides chemical insights about the mechanism of thermal decomposition and breakdown products that are unavailable by experimental techniques. This ability to explore the relationship between molecular structure and chemical and physical properties allows for a more systematic approach to the design of new polymers and processes.
This application note describes an effective approach to predicting thermal stability and understanding degradation mechanisms of polymers, using polyolefins as an example. (More than half of all plastics produced are polyolefins.)
As a general rule, and in the interest of speed, one starts by building the smallest model compound that realistically represents the properties to be investigated. Polymers differ from small molecules, in that they consist of long chains that are only as strong as their weakest link: thermal stability does not necessarily reflect the strength of the dominant bond type, it is limited by the strength of the bond that requires the least energy to break. This is frequently due to an irregularity. There is also the fact that polymers are massive molecules with limited mobility due to their size and chain entanglements. To realistically represent this, it is necessary to model several repeat units, at least for polypropylene. In the absence of specific reactions, such as elimination retro Diels-Alder, Ene reaction, etc., the initial step in any thermal process is going to be the homolysis of a bond. Since this is an electronic process; ie. a redistribution of electrons into a new set of orbitals, an electronic method is required to model the process. By using Quantum Mechanics to model the breaking of each bond type in a given polymer, one can directly predict the energy barrier for each bond dissociation.
Comparing the relative barriers to dissociation identifies the weakest bond and the limit to stability. One approach would be to model an oligomer, and calculate the relative energies of each pair of radicals that could from by breaking a bond. Comparing the energy differences would identify the weakest bond based on a thermodynamic barrier for homolytic bond dissociation: it assumes the energy rises as the atom distance increases from the normal bond distance to asymptotically approach the energy of the separated free radicals in the limit.
An alternative approach is to compute a complete reaction diagram for each bond homolysis. The transition state (if any) is identified, and its energy, relative to the ground state of the oligomer, is the kinetic barrier to homolysis. This latter approach is more appropriate for polyolefins, and is illustrated for polypropylene and polybutene in the following.
The basis of the approach is a quantum mechanical calculation using MOPAC. An optimized reaction coordinate is run using a MOPAC PM3 UHF calculation. The UHF model was taken, to provide a smooth transition in going from the fully paired configuration of electrons in the polymer ground state, to the separated pair of radical intermediates, each with an unpaired electron. AM1 calculations on free radicals are typically accurate to about 8 kcal/mole. By focusing on energy differences, systematic errors tend to cancel, so that relative energies are more accurate than absolute energies.
In one sense, Polyolefin thermal stability is a simple system, because there are only C-C bonds in the backbone. As it turns out, however, some interesting subtleties lead to significant effects on stability. The first of these has to do with the stereochemistry. Isotactic polypropylene (the major form of polypropylene produced commercially) has each monomer unit incorporated with the same orientation as the preceding monomer. This does not mean that all of the methyl side chains are on the same side of the backbone, however. Instead, it's well known that the backbone bonds twist to form a helix with three monomer units per turn.
An isotactic polypropylene oligomer is easily built from an isopropyl fragment with a "Polymerize" type command, using a backbone dihedral angle of -60, after deleting the hydrogen anti to the vacant site on the secondary carbon, to generate the repeat unit.
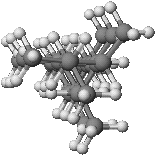
Molecular Mechanics geometry optimization with the MM2 Molecular Mechanics force field, correctly identifies the helical geometry (see Figures 1 and 2 on the front page) to be significantly more stable than a straight chain conformation (by about 8 kcal per turn of the helix). This geometry is used as the starting point for calculating the relative energy barriers to bond homolysis in MOPAC.
An optimized search generates a reaction diagram such as the one shown for homolysis of an anti backbone bond in Figure 3. The weakest bond is identified as the one with the lowest energy barrier.
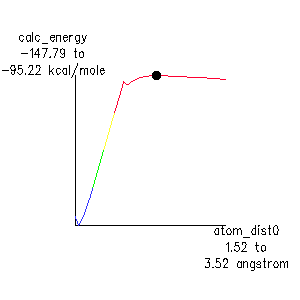
The first observation is that energy does not simply rise to approach the energy of the separated free radicals in the limit: the energy actually goes through a shallow maximum. In fact, this is a true transition state: a MOPAC Force calculation shows one and only one negative vibrational frequency. By doing an IRC calculation, and visualizing the movement around the transition state (3-D stereo capabilities are especially helpful), it is easy to recognize that one difference between the polymer and small molecules is that the two polymer halves hold back the carbons in the bond as it is being broken, and don't allow them to finish rehybridizing until the two bulky polymer fragments disengage. This is shown in the static images of the ground state , transition state , and free radical intermediates in Figure 3 above. The calculated activation enthalpy, 52.6 kcal., is in good agreement with literature estimates of 55-65 kcal.
A second insight, is that although each monomer in isotactic polypropylene is incorporated with the same orientation, and each backbone bond has one secondary carbon and one tertiary carbon, there are, in fact, two distinct types of backbone bond: locked in either a gauche or an anti conformation. The calculated energy difference of 2.5 kcal means there are alternating strong-weak backbone bonds, with about one order of magnitude difference in their halflives at the melting point of polypropylene!
The importance of balancing the choice of QM method with the size of the model compound to realistically represent the polymer can be demonstrated at this point. Trying to study this alternating strong-weak backbone bond phenomenon with an ab initio QM method, even doing only the minimum pair of 6-31G* optimizations, modeling a tetramer takes six CPU days on a modern workstation. This is in comparison to one CPU day to run two complete, optimized reaction coordinate searches on an octamer semi-empirically. More importantly, simplifying the model to a tetramer no longer includes the effect of the helix. There is no longer a maximum in the energy diagram, nor is there a difference between the gauche and anti backbone bond barriers! The octamer appears necessary to realistically represent the polymer, but this is impractical to do at the ab initio level.
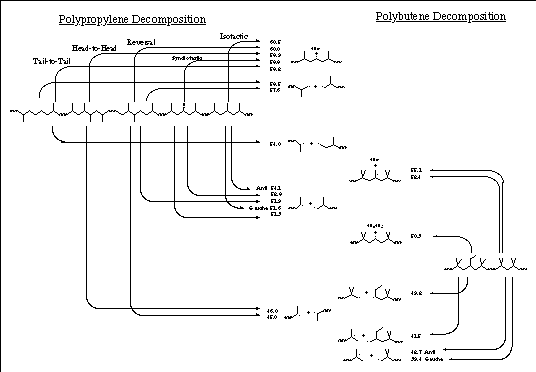
A third insight comes from this modeling: polymerization irregularities can induce a weak link which could reduce the thermal stability of polypropylene by two orders of magnitude in polymer halflife. This agrees with the observation that polypropylene, like most polymers, decomposes at a temperature substantially lower than comparable small molecules when there are irregularities that can act as weak points where degradation starts. Only irregularities that include a head-to-head link have this large an effect, however. See Figure 4 following.
Additional insights come from a similar analysis of polybutene bonds and comparing those calculations with the polypropylene results. A perfectly regular n-butene/isobutene alternating copolymer has some bonds that are as strong as in polypropylene, but the other bonds, especially with irregularities, in the polybutene make it inherently less stable thermally than even a completely irregular polypropylene by two orders of magnitude. (As with polypropylene, homolysis of a side chain is a higher energy process than homolysis of a backbone bond.)
The thermal stability of polyolefins can be readily modeled semi-empirically with Mopac. Initial fragmentation patterns and relative polymer stabilities can be predicted. Even relatively subtle effects, including deviation from small molecule behavior can be studied.
